Updating a phylogenetic tree

Interface

MolecularEvolution.AbstractUpdate Type

Summary

abstract type AbstractUpdate <: Function

A callable type that typically takes (tree::FelNode, models; partition_list=1:length(tree.message)), updates tree and models, and returns the updated tree and models.

Example

Define a new subtype, where foo and bar are arbitrary updating functions

struct MyUpdate <: AbstractUpdate end

function (update::MyUpdate)(tree::FelNode, models; partition_list=1:length(tree.message))
    tree, models = foo(tree, models, partition_list=partition_list)
    tree, models = BayesUpdate(nni=0)(tree, models, partition_list=partition_list)
    tree, models = bar(tree, models, partition_list=partition_list)
    return tree, models
end

See also: StandardUpdate

source

MolecularEvolution.StandardUpdate Type

Summary

struct StandardUpdate <: AbstractUpdate

A standard update can be a family of calls to nni_update!, branchlength_update!, root_update!, and model updates.

Constructor

StandardUpdate(
    nni::Int,
    branchlength::Int,
    root::Int,
    models::Int,
    refresh::Bool,
    nni_selection::Function,
    branchlength_modifier::UnivariateModifier,
    root_update::RootUpdate,
    models_update::ModelsUpdate
)

Arguments

• nni::Int: the number of times to update the tree by nni_update!

• branchlength::Int: the number of times to update the tree by branchlength_update!

• root::Int: the number of times to update the tree by root_update!

• models::Int: the number of times to update the model

• refresh::Bool: whether to refresh the messages in tree between update operations to ensure message consistency

• nni_selection::Function: the function that selects between nni configurations

• branchlength_modifier::UnivariateModifier: the modifier to update a branchlength by branchlength_update!

• root_update::RootUpdate: updates the root by root_update!

• models_update::ModelsUpdate: updates the model parameters

See also: BayesUpdate, MaxLikUpdate

source

Example

using MolecularEvolution, Plots, Distributions

Simulate a tree

tree = sim_tree(n = 50)
initial_message = GaussianPartition()
models = BrownianMotion(0.0, 1.0)
internal_message_init!(tree, initial_message)
sample_down!(tree, models)
log_likelihood!(tree, models)

-43.1267338778611

Add some noise to the branch lengths

for n in getnodelist(tree)
    n.branchlength += 100 * rand()
end
log_likelihood!(tree, models)

-164.422369424674

Optimize under the brownian motion model

update = MaxLikUpdate(branchlength = 1, nni = 0, root = 1)
tree, models = update(tree, models)
@show log_likelihood!(tree, models)

-18.562365365312395

Set up a Bayesian model sampler

Let's assume the target of inference is not the tree itself, but rather the models. Assume further that you want to, for a fixed mean drift, sample the variance of the brownian motion model, with the metropolis algorithm. We begin with a struct that defines the model and how it's updated

tree = sim_tree(n = 200)
internal_message_init!(tree, GaussianPartition())
#Simulate brownian motion over the tree
models = BrownianMotion(0.0, 2.0)
sample_down!(tree, models)
mutable struct MyModelSampler{
    T1<:ContinuousUnivariateDistribution,
    T2<:ContinuousUnivariateDistribution,
} <: ModelsUpdate
    acc_ratio::Tuple{Float64, Int64, Int64}
    log_var_drift_proposal::T1
    log_var_drift_prior::T2
    mean_drift::Float64
    function MyModelSampler(
        log_var_drift_proposal::T1,
        log_var_drift_prior::T2,
        mean_drift::Float64,
    ) where {T1<:ContinuousUnivariateDistribution, T2<:ContinuousUnivariateDistribution}
        new{T1, T2}((0.0, 0, 0), log_var_drift_proposal, log_var_drift_prior, mean_drift)
    end
end

Then we let this struct implement our metropolis_step interface

MolecularEvolution.tr(::MyModelSampler, x::BrownianMotion) = log(x.var_drift)
MolecularEvolution.invtr(modifier::MyModelSampler, x::Float64) =
    BrownianMotion(modifier.mean_drift, exp(x))

MolecularEvolution.proposal(modifier::MyModelSampler, curr_value::Float64) =
    curr_value + rand(modifier.log_var_drift_proposal)
MolecularEvolution.log_prior(modifier::MyModelSampler, x::Float64) =
    logpdf(modifier.log_var_drift_prior, x)

Now we define what a model update is

function (update::MyModelSampler)(
    tree::FelNode,
    models::BranchModel;
    partition_list = 1:length(tree.message),
)
    models = metropolis_step(update, models) do x::BrownianMotion
        log_likelihood!(tree, x)
    end
    log_likelihood!(tree, models, partition_list = partition_list) #refresh messages
    return models
end

Now we define how the model is collapsed to its parameter

function MolecularEvolution.collapse_models(::MyModelSampler, models::BranchModel)
    return models.var_drift
end

Now we define a Bayesian sampler

update = BayesUpdate(
    nni = 0,
    branchlength = 0,
    models = 1,
    refresh = true,
    models_sampler = MyModelSampler(Normal(0.0, 1.0), Normal(-1.0, 0.2), 0.0),
)
trees, LLs, models_samples = metropolis_sample(
    update,
    tree,
    BrownianMotion(0.0, 7.67),
    1000,
    burn_in = 1000,
    collect_LLs = true,
    collect_models = true,
)

ll(x) = log_likelihood!(tree, BrownianMotion(0.0, x))
prior(x) = logpdf(update.models_update.log_var_drift_prior, log(x)) - log(x)
x_range = 0.1:0.1:5

p1 = histogram(
    models_samples,
    normalize = :pdf,
    alpha = 0.5,
    label = "Posterior samples",
    xlims = (minimum(x_range), maximum(x_range)),
    xlabel = "variance per unit time",
    ylabel = "probability density",
)
p2 = plot(x_range, ll, label = "Tree likelihood")

p3 = plot(x_range, prior, label = "Prior")
plot(p1, p2, p3, layout = (1, 3), size = (1100, 400))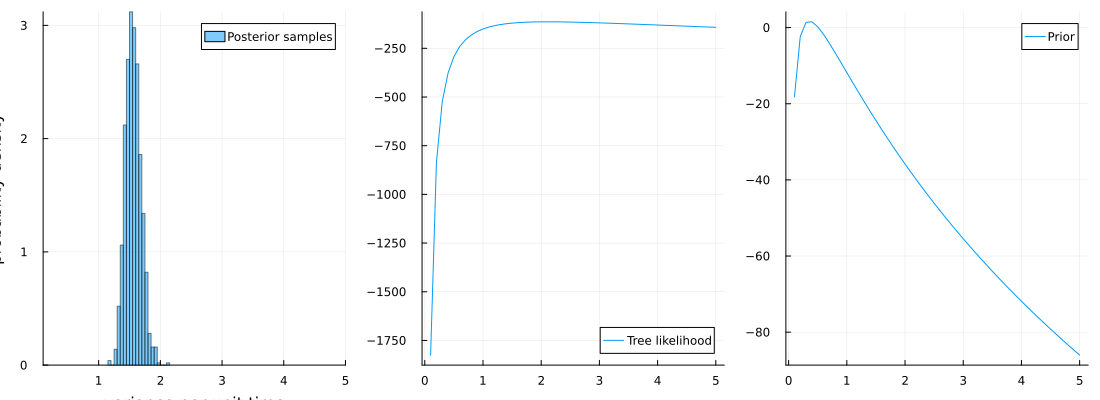

plot(LLs)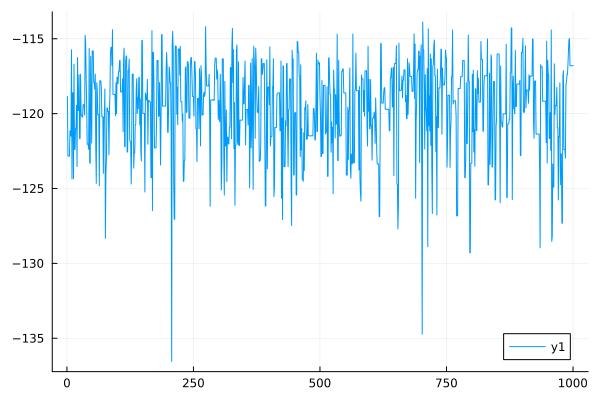

plot(models_samples)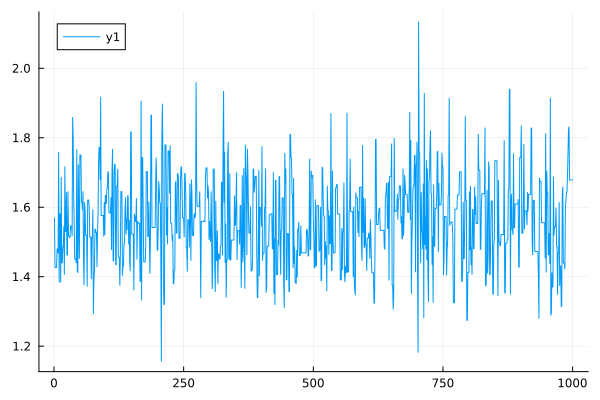

---

This page was generated using Literate.jl.